Home

Process Reward Models (PRMs) have emerged as a crucial tool for improving the reliability of Large Language Models (LLMs) in complex reasoning tasks by providing step-level supervision rather than just evaluating final answers. However, current PRM training methods face significant limitations: they rely on expensive manual annotations for step-level supervision and struggle to generalize beyond their training distribution, particularly when encountering subtle or novel reasoning errors.

This paper introduces Adversarially Trained Process Reward Models (APRM), which reframes PRM training as a two-player game between a Generator that creates deceptive reasoning errors and a Reward Model that learns to detect them. The approach eliminates the need for costly human annotations while creating an adaptive curriculum of increasingly challenging negative examples that improve the PRM's robustness and generalization capabilities.

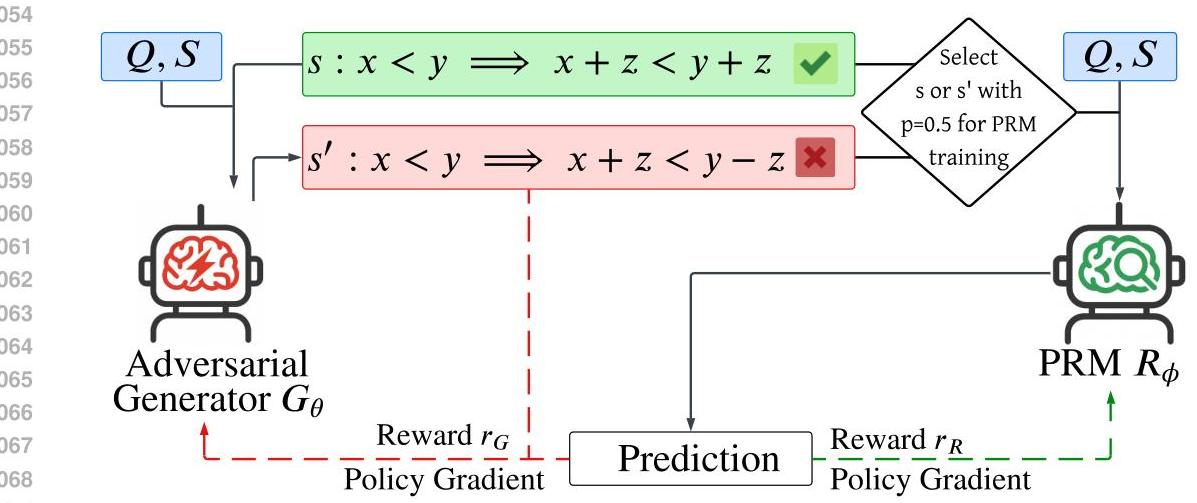
Figure 1: The APRM framework showing the adversarial interaction between the Generator (red) and Process Reward Model (green). The Generator corrupts correct reasoning steps while the PRM learns to classify their correctness, creating an adaptive training curriculum.

Problem Formulation and Game-Theoretic Framework

The core innovation lies in formulating PRM training as a general-sum, non-cooperative game between two neural agents. The Generator (\(G_\theta\)) aims to perturb correct reasoning steps into plausible but incorrect ones that can fool the Reward Model (\(R_\phi\)). Meanwhile, the Reward Model learns to accurately classify the correctness of reasoning steps, including the increasingly sophisticated errors produced by the Generator.

This setup differs fundamentally from traditional adversarial training in several ways. Unlike zero-sum games such as GANs, APRM employs asymmetric reward functions that create a general-sum game structure. The Generator receives rewards based on whether it successfully fools the Reward Model with incorrect steps:

\[ r_G = \begin{cases} +1 & \text{if } y = 0 \text{ and } y' = 1 \text{ (successful deception)} \\ 0 & \text{if } y = 0 \text{ and } y' = 0 \text{ (detected error)} \\ -1 & \text{if } y = 1 \text{ (failed to corrupt)} \end{cases} \]

The Reward Model receives simpler binary feedback for correct classification:

\[ r_R = \begin{cases} +1 & \text{if } y = y' \text{ (correct classification)} \\ -1 & \text{if } y \neq y' \text{ (incorrect classification)} \end{cases} \]

where \(y\) represents the true correctness and \(y'\) represents the model's prediction.

Theoretical Foundations and Convergence Guarantees

A key strength of this approach is its solid theoretical foundation. The paper proves the existence of Nash Equilibria for the regularized game and establishes linear convergence rates when using appropriate optimization techniques. Both players optimize regularized utility functions that include KL divergence penalties and entropy bonuses:

\[ U_i^{\text{reg}}(\pi_i, \pi_{-i}) = U_i(\pi_i, \pi_{-i}) - \tau \cdot KL(\pi_i \,\Vert\, \pi_i^0) + c_H \cdot H(\pi_i) \]

This regularization serves multiple purposes: preventing mode collapse, ensuring exploration, and inducing strong concavity in individual player objectives. The strong concavity property makes the overall game strongly monotone, which enables the use of game-aware optimizers like Optimistic Gradient Descent-Ascent (OGDA) with provable linear convergence to the Nash Equilibrium.

The theoretical analysis demonstrates that unlike zero-sum games that converge to saddle points, this general-sum formulation converges to stationary points that represent Nash Equilibria, providing a more appropriate solution concept for the PRM training objective.

Training Methodology and Implementation

The practical implementation combines reinforcement learning with game-theoretic optimization. Both the Generator and Reward Model use Llama-3.1-8B as their backbone architecture and are trained using Proximal Policy Optimization (PPO) augmented with OGDA updates. The training alternates between players, with one model updated for 5 gradient steps while the other remains frozen.

A crucial component is the Ground-Truth Correctness Oracle, which uses algorithmic verification rather than LLM-based evaluation to determine the true correctness of generated steps. This oracle employs multiple verification methods including cosine similarity, entity matching, logical operation validation, and structural consistency checks to provide objective ground truth for the adversarial training process.

The Reward Model is trained on a carefully balanced mixture of data: 50% gold solution steps from the MATH dataset and 50% negative examples generated by current and past versions of the Generator. This mixture prevents the model from forgetting how to detect simpler errors while continuously adapting to new, more sophisticated ones.

Experimental Results and Performance Analysis

The experimental validation demonstrates substantial improvements across multiple mathematical reasoning benchmarks. APRM achieves an average improvement of +3.4 percentage points over the strongest trained PRM baseline (ReST-MCTS) and +4.2 percentage points over the best prompting methods across five diverse benchmarks (MATH500, JEEBench, OlympiadBench, AIME25, AMC).

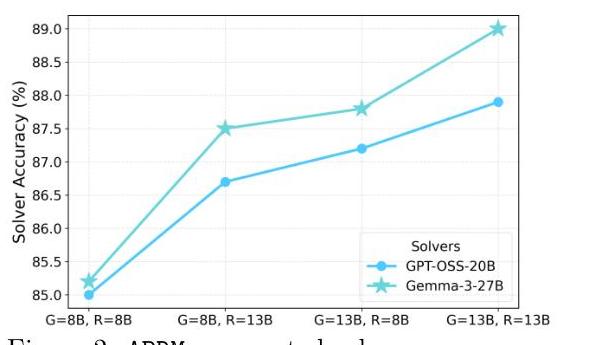
Figure 2: APRM performance scaling with Generator and Reward Model capacity. Increasing Generator capacity yields larger improvements than increasing Reward Model capacity, suggesting the importance of diverse error generation.

Particularly notable is APRM's superior performance on out-of-distribution tasks. On JeeBench, an out-of-distribution benchmark, APRM outperforms ReST-MCTS by +5.3 percentage points, demonstrating significantly better generalization capabilities. The method also shows strong cross-domain transfer, with consistent improvements on SciBench, a scientific reasoning benchmark spanning multiple science domains.

An important finding is that APRM's effectiveness increases with solver model capacity. While traditional PRMs often show diminishing returns or even degraded performance with larger solvers, APRM maintains and enhances its benefits as solver capability grows. This suggests that adversarial training creates PRMs robust enough to handle the more sophisticated but potentially more error-prone outputs of larger models.

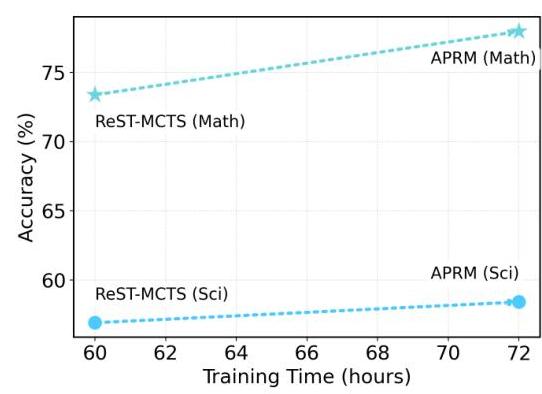
Figure 3: Training time comparison showing APRM's efficiency relative to baseline methods across mathematical and scientific reasoning tasks.

Qualitative Analysis and Error Evolution

The qualitative analysis reveals the sophisticated evolution of the Generator's error-making capabilities. Initially, the Generator produces trivial mistakes like basic arithmetic errors. As training progresses, it learns to generate locally consistent but globally incorrect reasoning steps. In advanced stages, the Generator creates subtle conceptual errors such as applying incorrect probability principles or making sophisticated logical fallacies that require deep domain understanding to detect.

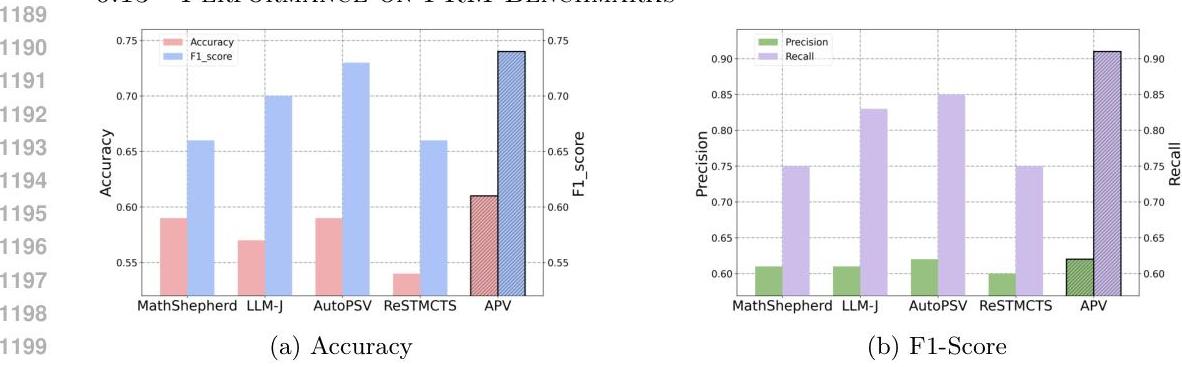
Figure 4: APRM performance on PRM evaluation metrics, showing superior accuracy, precision, recall, and F1-score compared to baseline methods.

This evolution demonstrates the adaptive curriculum effect: as the Reward Model becomes better at detecting certain types of errors, the Generator is forced to discover new, more subtle forms of incorrectness. This creates a continuous learning dynamic that pushes both models toward higher levels of sophistication.

Limitations and Future Directions

The paper acknowledges several limitations. The primary constraint is computational cost – while inference remains unchanged, the adversarial training process requires more resources than static dataset training. However, this represents a one-time training cost that yields long-term benefits in PRM quality and reduced dependence on human annotation.

Another limitation involves the Generator's difficulty in creating targeted errors for complex theorem preconditions, such as properly checking whether conditions for applying specific mathematical theorems are satisfied. This suggests areas for future improvement in oracle design or Generator architecture.

Significance and Impact

APRM represents a significant advancement in making LLM reasoning more trustworthy by addressing two critical bottlenecks in current PRM training: the cost of human annotation and poor generalization to novel errors. The approach's theoretical grounding, combined with strong empirical results, positions it as a robust framework for building reliable Process Reward Models.

The methodology's core principles extend beyond mathematical reasoning to any domain where step-level supervision is valuable but expensive to obtain manually. Potential applications include complex coding tasks, scientific discovery, legal reasoning, and medical diagnosis – any field where subtle errors can have significant consequences and where building adaptive curricula of challenging examples could improve model robustness.

By providing a theoretically sound and empirically validated approach to adversarial PRM training, this work opens new avenues for enhancing the reliability and trustworthiness of large language models across diverse high-stakes applications.